Zero Knowledge Proofs Part One: The Cryptographic Protocols and Their Variations

Blockchain Technology 12 min, 26 sec READ

by Martin Banov

Part 1: A brief overview of zero-knowledge proof protocols and their applications in blockchain-based systems (e.g., zk-SNARKs, zk-STARKs).

This is part one of a two-part series on zero-knowledge proofs. Part two will examine the implementations and applications of zero-knowledge proof protocols by Zcash, Ethereum, Aztec, Coda, Leverj, REN Project and more. 

Zero-knowledge proofs are a family of cryptographic protocols whose value lies in their seemingly paradoxical attribute of proving a statement without revealing anything about it (that is, proving its validity without revealing it itself or anything else about it). On the surface, it appears as if a verifier given a zero-knowledge proof (ZKP) is supposed to be told by God that this is so. However, God, in such a setting, functions as the underlying protocol that both Alice and Bob (A and B) follow (or Peggy and Victor, in a ZK context, for Prover and Verifier). Importantly, for the purpose of blockchains in their institutional roles, zero-knowledge constructions enable malicious actors to be forced into a protocol whereby they execute in accordance with predetermined steps to ensure security and enforce honest behavior within otherwise non-transparent privacy.

Zcash is the first and perhaps the most popular crypto-currency to implement zero-knowledge cryptography as a means of upgrading the Bitcoin protocol with private and selectively disclosable (to, for example, auditors or regulators, should that be required) transactions, while nonetheless still taking place in accordance with the protocol (i.e., the transactions taking place, even though hidden, are guaranteed to be valid within the context in which they take place). ZClassic and ZenCash also derive from Zcash and make use of the same libraries (libsnark), while Ethereum has incorporated a broader implementation for use within dApps and contract code. Below we provide a quick overview of applications based on zero-knowledge schemes with accompanying examples so as to help one acquire a basic intuition of ZKP applications in distributed public networks.

A Bit of Background: The P and NP (Computational) Complexity Zoo

A few fundamental notions from computational complexity are important in order to acquire a good understanding of zero-knowledge proofs as they relate to public networks, distributed systems and their shared records. In computer science, P class problems refer to problems that can be solved by a reasonably fast program on a computer of some sort (e.g., a Turing machine). In other words such that there is an implementable solution, which can be refined in what is called polynomial time (in effect, synonymous with fast time). Roughly speaking, if one has to compute some value (and not "search" for something) the problem is usually a P class problem (e.g., verifying a Bitcoin transaction is a P class problem).

Most importantly, polynomial expressions (from Greek, “many names”) are not exponential functions (i.e., to the power of), but map to arithmetic circuit problems of linear, quadratic, cubic and similar types, where the number of (computational) steps required are acceptable compared to the size of the problem. That is to say, problems involving things like mazes, multiplication, subtraction, etc. - or that could otherwise be reduced or translated to instances of such problems.

In the fabric of distributed ledgers, where the records of events or transactions are massively replicated among peers reproducing the same outputs (similar in principle to how lie-detector polygraphs operate), it is important that the number of computational steps in a set of executable instructions on-chain is kept at the minimum necessary to carry out what it is meant to. This is why zero-knowledge proofs in such (block-chained) environments need to be “succinct” and not require reproducing the execution of a program (i.e., set of instructions, smart contract or script) on-chain by an entire world in order to demonstrate or verify the validity of that execution.

The NP (for non-deterministic polynomial time) complexity class, on the other hand, describes problems where the soundness of their solutions have proofs which can be efficiently verified by deterministic computations in said polynomial time (as is usually the case of most blockchain-based systems, being deterministic and synchronous). That is, the mental work necessary for solving a particular problem can be reduced or translated to a simpler problem or set of problems (e.g., P problems) which is then capable of mechanizing the process of thinking that unfolds a particular binary decision tree. That way zero-knowledge proofs can be extended to any problem that falls in the NP class (practical zkSNARKs can be applied to all problems in NP in a generic fashion).

And since blockchains as such require strict determinism to maintain the integrity of global consensus (the same input must always reproduce the same output with no deviation), they scale much better if engaged to only verify/read instead of execute/write. Zero-knowledge (ZK) constructions in this scenario allow for optimizing a solution which utilizes the blockchain as a verifier of general computational integrity off-chain, with verification times on-chain magnitudes faster than execution times - in the logarithm (that is, the inverse of exponentiation) of the steps or cycles involved (measured in gas expenditure on the Ethereum blockchain).

Zero-Knowledge Proofs: Basic Conditions and Defining Properties 

Zero-knowledge proofs are, in essence, cryptographic constructions which investigate how far formal logic can be taken in solving tricky problems. In a ZKP a prover, Peggy and a verifier Victor (in place of the proverbial Alice and Bob) interact in a series of steps in such a way that Peggy is able to prove to Victor the validity of some statement without revealing anything about that statement, given that both follow the rules or constraints of the same protocol.

The basic intuition is commonly illustrated with the anecdote of Ali Baba's cave. Imagine a ring-shaped cave with an entrance and a magic door inside on the other end obstructing the sides, as shown below.

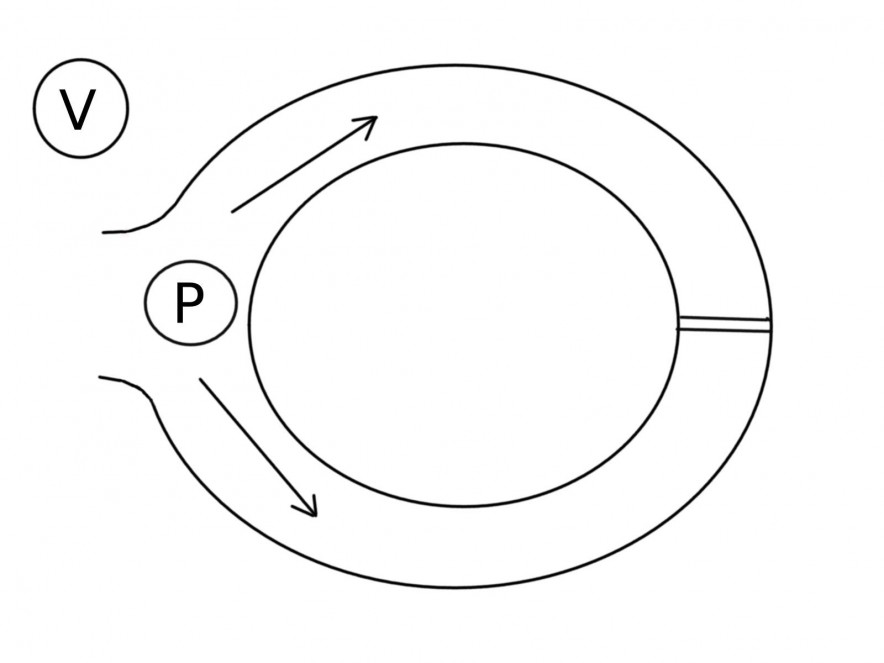
Peggy wants to prove to Victor her knowledge of the secret phrase that opens the door, but in a way that wouldn't reveal the phrase itself. So, Victor waits outside a bit, then walks in and shouts which side he wants Peggy to show up from. This is repeated until the probability of Peggy simply having turned out lucky approaches zero. Such scenario exemplifies interactive zero-knowledge proofs (ZKPs), while non-interactive ZKPs usually rely on a common reference string (CRS) both parties share (and thus don't require any interactive rounds).

The concept of interactive zero-knowledge proof systems and probabilistic protocols was first proposed by Shafi Goldwasser and Silvio Micali in the late 1980s, and the general assumption of how the proof of a given statement as such contains more knowledge than the sole true/false value or validity of that statement (making use of things like auxiliary inputs, “trapdoors”, etc.) underpins much of modern cryptography since.

A zero-knowledge proof must by definition satisfy the following three properties:

• Completeness: If a statement is true and both parties follow the same protocol correctly, then the verifier naturally becomes convinced. If the prover is being honest and providing an authentic, legitimate proof, the verifier will be eventually convinced (with high probability).
• Soundness: If a statement is false, the verifier will almost certainly not be convinced (Probabilistically Checkable Proof constructions rely on the strong evidence of high probability, i.e. repetition until the probability of falsehood or plain luck approaches zero) and no cheating prover can reliably convince an honest verifier that a false statement may be true. The soundness property, therefore, means that a zero-knowledge proof must not be able to prove false statements.
• Zero-knowledge: The verifier learns no further information (about the content of the statement). Micali and Manuel Blum further investigated the possibilities of saving up on computational resources by eliminating the interactive communication rounds (which tend to be the most computationally expensive), instead relying on a common reference string derived from a shared or public random beacon (for instance, the same Geiger counter).

In the past 30 years, research on zero-knowledge proof systems has been progressively improving with focus on optimizing their efficiency for specific problems and applications, making particular improvements in various different parameter scenarios. This has led to ZK schemes yielding dramatic reductions in the size of the proof as well as the length of the common reference string (in the case of non-interactive proofs that rely on them).

Two Types of Zero-Knowledge Constructions: zk-SNARKs and zk-STARKS

In the world of distributed ledgers and crypto-currency, two forms of ZK constructions are most commonly used in applications. Zcash is the first widespread application of zk-SNARKs (Succinct Non-Interactive ARguments of Knowledge), while zk-STARKs is a ZK mechanism developed by cryptographers and researchers in Technion (Israel Institute of Technology) that doesn't require a trusted setup (as SNARKs do, which in the case of Zcash is the well-known ceremony), is quantum-proof and significantly faster to generate.

zk-SNARKs: Zero-Knowledge Succinct Non-Interactive ARguments of Knowledge  

“If I had but the time and you had but the brain.”

       - Lewis Carroll, The Hunting of the Snark

Zk-SNARKs are particular ZKP schemes and the first kind of ZKPs to be incorporated within crypto-currency blockchain ledgers. A zk-SNARK construction as such involves three algorithms:

• A key generator: Setting up the parameters for generating a key pair. For example, a trusted set of people generates a private/public key pair (as with the above mentioned Zcash ceremony), destroys the private shards and goes on to generate another key pair from the public key. This second key pair creates a proving and a verification key for some given program within that range.
• A prover: The prover takes the provided proving key, a given public input and a private witness (representing the satisfying assignment for the program/formula/algorithm at hand, verifying that a variable assignment satisfies the specific task and can be solved in polynomial time; the witness is usually generated along with the proof) and generates a proof.
• A verifier: Verification is computed from the verification key, the public input and the provided proof, evaluating to either true or false depending on whether the proof is correct or not (in the circumstance of what is being verified to satisfy what conditions). To render this more vivid, two polynomial strings are produced which are expected to not deviate much from agreeing most of the time, given legitimacy according to protocol. Then a series of quick random checks at arbitrary sites on the strings are performed to make sure they do agree.

While the above may sound a bit byzantine at first (and the mathematical underpinnings are undoubtedly complex, but we need not concern ourselves to that extent in order to grasp the basic reasoning behind it), it gradually starts making sense along the way and with particular examples and instances of real-world applications.  

zk-STARKs: Zero-Knowledge Succinct Transparent ARguments of Knowledge

The weakest point in zk-SNARK schemes is that they depend on an initial trusted setup phase (as already mentioned)  that could potentially be compromised. Additionally, zk-SNARKs are vulnerable to quantum attacks (since they rely on elliptic curve cryptography). A more recent innovation in zero-knowledge cryptography that resolves these issues is zk-STARKs (Zero-Knowledge Scalable Transparent ARguments of Knowledge).

Zk-STARKs are a faster, cheaper, quantum-proof alternative that doesn't require a trusted setup. Zk-SNARKs researcher Professor Eli Ben-Sasson explains,

zk-SNARKs use asymmetric public key cryptography to establish security. zk-STARKs instead requires a leaner symmetric cryptography, namely, collision resistant hash functions, and thus removes the need for a trusted setup. These same techniques also eliminate the number-theoretic assumptions of zk-SNARKs that are computationally expensive and prone to attack by quantum computers. This makes zk-STARKs both faster to generate and post-quantum secure.

ZkSNARKs are to be eventually upgraded to zkSTARKs in many of the present applications. The 80-page long paper co-authored by Prof. Eli Ben-Sasson ("Scalable, transparent, and post-quantum secure computational integrity") that describes the protocol in depth is available here.

That concludes part one of this two-part series on zero-knowledge proofs. Part two will examine the implementations and applications of zero-knowledge proof protocols by Zcash, Ethereum, Aztec, Coda, Leverj, REN Project and more. 

Links and Resources

ZoKrates Gitter and documentation (for zkSNARK constructions on Ethereum).

Clipperz.is is a nice example of a simple SKP app - a zero-knowledge password manager and confidential data vault written in Javascript. Everything submitted is locally encrypted by the browser before transmitted with the passphrase known only to the user client-side. 

Zeroknowledge.fm is podcast focusing on DLT and ZKP applications.  

Zcash public forum and Rocket chat.

A primer on ZKP by Matthew Green. 

"ZkSNARKs in a Nutshell", a great explanatory paper by Christian Reitwießner.

Horizen (formerly ZenCash) official site.

ZClassic official site.